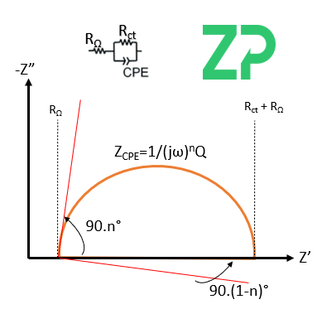
Depressed semicircle behaviour is explained by the ZARC element. The constant phase element (CPE) is one of the most common circuit elements which exists to describe capacitance.
The ZARC element describes the double-layer capacitance and charge transfer at an electrode-electrolyte interface. It is a parallel connection between an ohmic resistor and a constant phase element (CPE). This element is given by Equation 1:
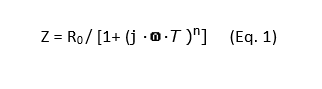
It has been cited that Z can be found by parallel combination of a CPE and a resistor to give Equation 2:
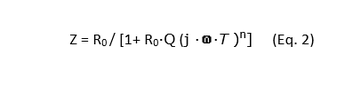
By doing this, Equation 1 and 2 are interchangeable if Equation 3 is defined as:
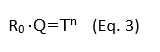
Using Equation 1 is advantageous as it allows us to shift from thinking in terms of a distribution of capacitance to a distribution of time constants (T). It has been proven that if the probability of finding an activation energy is given by Equation 4 and the time constant T is given by Equation 5, then Z will follow Equation 1 and a depressed semicircle is observed.
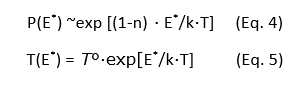
Additionally, considering T(E*) as R(E*) ·C, then RF (the faradaic resistance) depends on the activation energy. It is also possible for polycrystalline metal electrodes to exhibit ZARC element behaviour. The capacitance of different crystal faces may differ and the different states of oxidation on a carbon surface influences the electron transfer rate constants.
